Номограмма для определения тангенса, синуса и косинуса острого угла графическим способом (т.е. приблизительные значения)
Для получения числовых значений тригонометрических функций геометрическим способом, используется "единичная окружность" (« тригонометрический круг » с центром в начале координат и радиусом равным единице).
Отрезок, соединяющий точку на единичной окружности с началом координат, и
находящийся под острым углом поворота "а" относительно положительной полуоси абсцисс (по оси x) и ординат (по оси y), имеет проекции на эти оси (так называемый, вертикальный и горизонтальный диаметр единичного круга):
sin(а) = y ("вертик-й диаметр единичной окружности", т.е. ордината точки на ед-й окр-ти)
cos(а) = x ("гориз-й диам. ед. окр-ти", т.е. абсцисса точки)
Линия тангенса – это касательная к единичной окружности, проведенная через правую крайнюю точку горизонтального диаметра ("точка касания"). Тангенс (лат. tangens - касающийся) – это вертикальный отрезок на линии тангенса между точкой касания и точкой пересечения линии тангенса и продолжения линии радиуса.
Данная функция имеет широкое практическое применение, например, в топографии и в навигационных расчётах – при измерении расстояний.
Примеры:
tg(45°) = 1
tg(60°) ~ 1.73
sin(55°) ~ 0.82
cos(55°) ~ 0.57
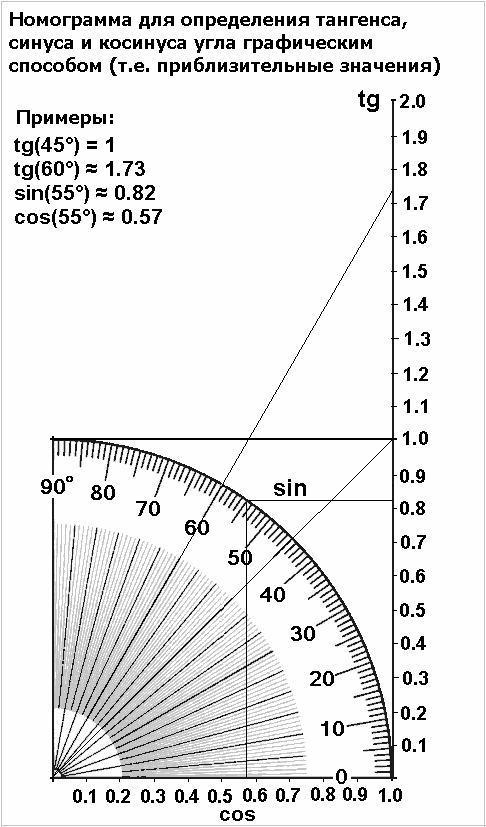
Рис.1. Номограмма-расчётчик для быстрого определения тангенса, синуса и косинуса острого угла графическим методом (чтобы найти приблизительные значения). Её можно бесплатно распечатать на принтере или самостоятельно нарисовать на тетрадном листе, линованном в клетку. Для изготовления самодельной номограммы, понадобятся: линейка, угольник и циркуль.
Чтобы самостоятельно построить большой транспортир и точный полевой угломер, с наименьшими делениями, проставленными через 15 угловых минут, нужно начертить окружность радиусом 57.3 сантиметров. Через интервалы, длиной 1см – ставятся и подписываются, как на рисунке 1, градусные штрихи (всего их должно быть 360 штук на полном круге). Каждый интервал, равный 1°, делится пополам и середина отмечается риской – это половина градуса (30'). И снова делится поровну, чтобы получить четвертные деления (15').
Если в наличии имеется только блокнотный лист, линованный в клетку и остро отточенный карандаш, то и без инструментов и без других канцелярских принадлежностей можно изготовить небольшой самодельный транспортир для грубых измерений. Для этого, обрывок листа из блокнота, сложенный в виде полоски – используется в качестве линейки (линии сетки проведены через 5 мм). Циркулем, который можно сделать из подручных материалов – строится окружность диаметром 57,3 или 114,6 миллиметров.
Через интервалы, длиной 1 или 2 сантиметра – проставляются и оцифровываются десятиградусные штрихи.
Меньшие доли – определяются интерполяцией.